Previous: Perfect correlations and disastrous outcomes | Next: Confessions under torture: how p-hacking forces data to lie
Your data science team just delivered amazing news. They've built a machine learning model that predicts customer churn with 99.8% accuracy on your historical data. The model captures every quirk of your past customers, patterns no analyst even saw.
"This is incredible!" you think. "We're going to save millions in retention costs!"
You deploy the model in production, confident that you've solved customer churn forever.
Three months later, the model is performing worse than a coin flip.
What happened? You just fell prey to one of the most seductive and dangerous statistical traps: overfitting.
What overfitting really means
Overfitting is like having a student who memorizes every answer on practice tests but completely fails when faced with new questions. The model becomes so perfectly tailored to your specific historical data that it loses the ability to generalize to new situations.
To understand overfitting, let's introduce two crucial concepts:
Training set: The historical data used to build and tune your model
Testing set: Fresh data used to evaluate how well your model actually works
The goal is to create a model that performs well on both sets of data, proving it can handle new, unseen situations. Overfitting happens when your model becomes excessively customized to the training set and completely gives up on generalizing to new data.
The Jerry disaster
Remember the dramatically overfit customer churn model we started with?
It was all because of Jerry, a well-meaning data analyst who learned this lesson the hard way.
Jerry's team was given ten days of customer data and tasked with predicting the next few data points. While everyone else was considering simple trends and seasonal patterns, Jerry got excited about showing off his advanced mathematical skills.
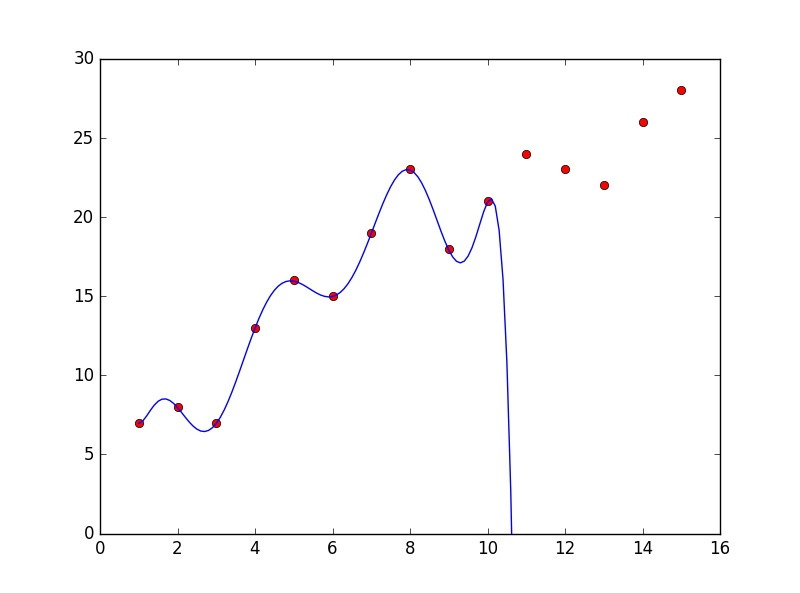
"I've found the perfect model!" Jerry announced, presenting this chart:
Jerry had discovered a 10th-degree polynomial that fit the ten data points with perfect accuracy. Not a single point was off by even a fraction. His model had zero error on the training data.
The rest of the team was skeptical. "Maybe a simple linear trend would be more reliable?" they suggested.
But Jerry was adamant. "Look at this fit! It's mathematically perfect! How can you argue with perfection?"
Five days later, the new data came in:
Jerry's "perfect" model was completely wrong. The simple line that his colleagues suggested would have been much more accurate.
Spotting and preventing overfitting
Some heuristics for detecting and preventing these mistakes:
Perfect performance
If your model shows extremely high accuracy on historical data, be very suspicious. Real-world data is messy, and perfect fits are usually too good to be true. Always hold out some data completely separate for final testing, data that's never used for model training or parameter tuning and "held out" until the end.
Performance gaps
Train your model on 80% of your data, then test it on the remaining 20%. If there's a huge performance difference between the two sets, you're overfitting. Even better: instead of one train/test split, try multiple random splits. If your model performance varies wildly across different splits, you're probably overfitting.
Excessive complexity
Begin with the simplest model that could possibly work. One heuristic: if you have more parameters than data points divided by 10, you're flying too close to the sun. A model with 50 parameters needs at least 500 data points. Only add complexity if it genuinely improves performance on held-out test data. Use regularization techniques that penalize overly complex models.
The grandma test
If your model makes predictions that don't make intuitive business sense, it might be picking up on noise rather than signal. Can you explain your model's key insights to your grandmother? If the model's logic doesn't make intuitive sense, be very careful before trusting it.
Hidden danger of overfitting
Overfitting is seductive because it makes you feel smart and successful. But, the most dangerous models are often the ones that work perfectly on historical data.
Before you deploy any predictive model:
Test it on completely fresh data
Start with simple approaches before getting fancy
Be suspicious of perfect or near-perfect performance
Make sure the model's logic passes the common sense test
Remember Jerry's lesson: mathematical perfection in modeling is often the enemy of practical success.
This is Part 3 of our 9-part series on statistical fallacies. Subscribe below for more:
Next time: We'll explore another trap that exploits our love of impressive-looking results: data snooping. I'll show you how searching through massive datasets for "significant" patterns almost guarantees you'll find meaningful-looking relationships that are actually pure noise.
Catch up on the entire series: